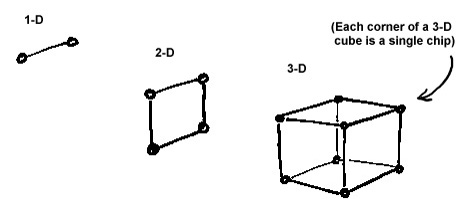
First 3 dimensions of a hypercube
The search for a form had to start with bare practicalities: how do you physically organize a machine with 65,536 processors? Is it physically possible to build it like a "normal" machine, or would we have to wallpaper a room with boards, and weave a rat's nest of cables between them?
The processors were grouped 16 to a chip, making a total of 4,096 chips. These chips were to be wired together in a network having the shape of a 12-dimensional hypercube. The term "12-D," far from having to do with warp drives and extraterrestrials, had the mundane but complicated meaning that each computer chip would be directly wired to 12 other chips in such a way that any two chips - - and thereby the 16 processors contained in each chip -- could communicate with each other in 12 or less steps. This network would enable the rapid and flexible communication between processors that made the CM-2 so effective. (4)
Overwhelmed by the effort to visualize a 12-D connection scheme for 4,096 chips, I expressed my bemusement to Richard Feynman, the Nobel Prize-winning physicist who was helping us design the network. (His son Carl was working on the Connection Machine, and the project sounded so interesting that Richard asked if he could help too!) Feynman had the rare talent of being able to explain the most complicated things simply, and characteristically his reply to my complaint was, "Oh, that's easy!"
Feynman drew two chips and connected them to make a "1-D" cube. This is what we commonly call a "line." He then joined two 1-D cubes at their ends to make a "2-D" cube, what we commonly call a "square." Next he joined two 2-D cubes to make a "3-D" cube, which is the same as our usual understanding of a "cube:"

Then came the
difficult step into the 4th dimension: he connected the two 3-D
cubes at their ends, joining like corners to make a "4-D" cube, the
first stage of what is called a hypercube, a cube with more than 3
dimensions. Although this process can be repeated indefinitely, it
becomes increasingly difficult to visualize these multidimensional
structures in a 2-D drawing.
My solution was to twist the 4th dimension cube to the side of the 3rd dimensional cube and then apply a radical graphic simplification: I represented all dimensions greater than 3 as thick "hyperlines," and drew cubes as solid objects in order to visually simplify the resultant structures:
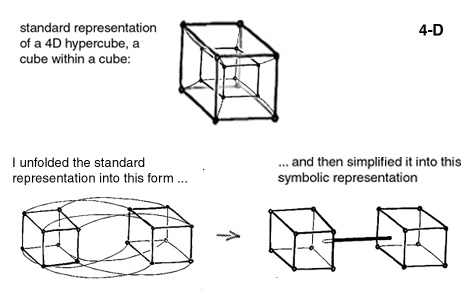
This symbolic representation has the added benefit of showing
in a glance that the structures
always repeat themselves: a 4-D hypercube looks just like a 1-D
line, except that it connects two cubes rather than two chips. A 5-
D hypercube is a square of cubes:
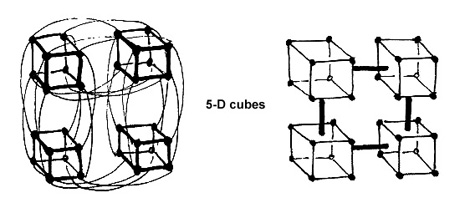
...and a 6-D hypercube is a cube of
cubes:
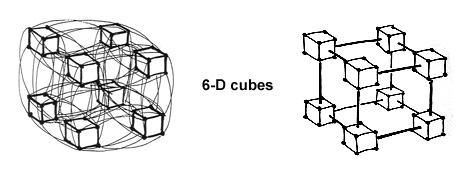
Going further, a 9-D hypercube is a cube of 6-D hypercubes:
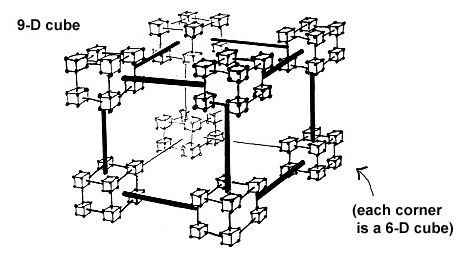
...and a 12-D hypercube is a cube of 9-D hypercubes:
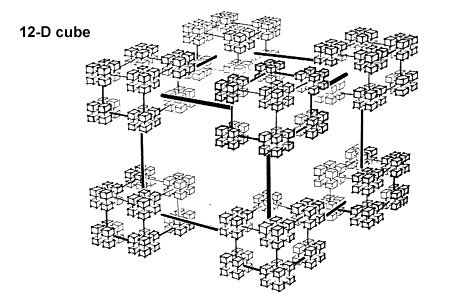
This is the
structure used in the CM-2, a cube with 2 to the power 12 corners,
or 4,096 chips, each connected to 12 other chips, each connection
being one dimension of the cube.
This structure was repeated throughout every level of the machine, in the traces connecting processor chips, in the connectors between the printed circuit boards, and in the 1,000 feet of cable connecting the highest dimensions of the machine. Once we understood this basic organizational principle, we could start to build the machine. Ted Bilodeau, working on the mechanical side, and Dick Clayton, working on the electrical side, were able to reduce the machine's original proportions from room-sized to machine-sized, using only standard, off-the-shelf computer packaging technology.
(previous) (next)